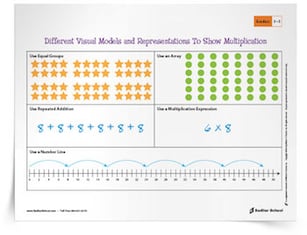
Students’ formal introduction to multiplication begins in the third grade, which lays the groundwork for solving all kinds of real-world problems. One critical aspect of multiplication is the concept of area models. This post looks at how to develop the concept of area models for multiplication and how to relate that concept to algorithms for finding the product of a two-digit by two-digit multiplication. The download for this post is a game that you can use in your classroom to practice multiplication with area models. Prior to third grade, students learn about addition and the concept of skip counting. Carefully structured activities, such as skip counting, lead to using an area model for multiplication. Students can arrange counters in equal numbers of rows and columns, labeling each row with the cumulative total. (For example, three rows of four can be sequentially labeled 4, 8, and 12). This arrangement of counters creates a rectangular array that can be interpreted as multiplication, which in turn leads to multiplication with area models.

In third grade, students should be using rectangular arrays to model multiplication facts within 100. This is the beginning of the formal use of multiplication with area models. You can see many examples of this in Progress in Mathematics, Grade 3, Chapters 4, 6, and 9. Standard 3.MD.7.A states: Find the area of a rectangle with whole-number side lengths by tiling it, and show that the area is the same as would be found by multiplying the side lengths. These tilings or arrays are the first step in developing an area model for multiplication.

A second major outcome of using arrays and area models for multiplication is the development of the idea of the distributive property. Standard 3.MD.7.C states: Use tiling to show in a concrete case that the area of a rectangle with whole-number side lengths a and b + c is the sum of a × b and a × c. Use area models to represent the distributive property in mathematical reasoning. If you are using the Progress in Mathematics series, a good place to address this would be after Chapter 9 Lesson 11, in conjunction with the lesson on area.

Fourth grade is where concepts of place value, multiplication with area models, and the distributive property come together. When students are beginning to extend multiplication to products beyond 100, they will find the production of rectangular arrays too cumbersome. (After all, who wants to draw the rectangular array for 15 x 17 and then count the squares?) At this time, teachers can introduce a new type of area models for multiplication where the individual tiles don’t have to be counted as shown in the diagram below. Given a choice between the array with counting all and the area model for multiplication, students will have the motivation to make the leap!

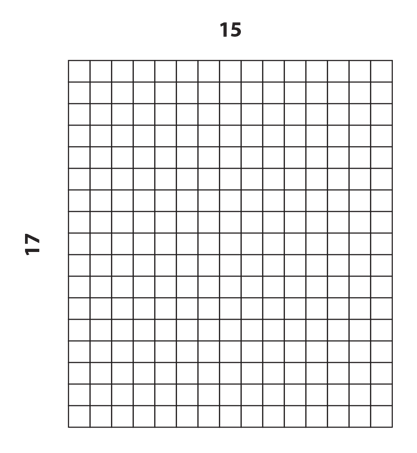
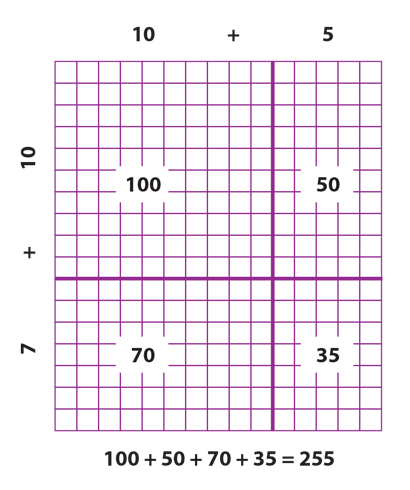
The real power of this area model for multiplication becomes evident when students begin to relate it to multiplication algorithms. Using the same example of 15 x 17, students can show how their diagram relates to the following algorithmic versions, first by using partial products, and then with the standard algorithm. The first step (partial products) looks this way:

The final step (the standard algorithm) then looks like this:

Chapter 4 of the Progress in Mathematics grade four curriculum is one place where you can extend the lessons to include the use of area models for multiplication.

Once your students have learned the technique of area models with multiplication, they will enjoy playing the printable game available for download.

RELATED RESOURCE: